内置图算法

GraphFrames实现了一些标准的图算法，包括：

• (1) 广度优先搜索(BFS)算法。
• (2) 连通分量算法。
• (3) 强连通分量算法。
• (4) 标签传播算法。
• (5) PageRank算法。
• (6) 最短路径算法。
• (7) 三角计数算法。

下面学习如何使用GraphFrames自带的这些图算法。

1. 广度优先搜索(BFS)算法

广度优先搜索算法（Breadth-First-Search，BFS），是一种图搜索算法。简单的说，BFS是从根节点开始，沿着树（图）的宽度遍历树（图）的节点。如果所有节点均被访问，则算法中止。BFS属于盲目搜索。

算法步骤如下：

• (1) 首先将根节点放入队列中。
• (2) 从队列中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
• (3) 若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
• (4) 重复步骤2。

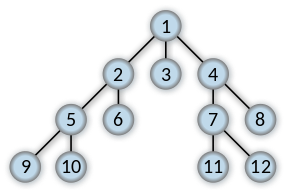
广度优先算法的遍历顺序为：1->2->3->4->5->6->7->8->9->10->11->12，如下图所示。

例如，要从g图对象中查找从源顶点为Esther、目标顶点（人）年龄小于32岁的用户，代码如下：

val paths = g.bfs.fromExpr("name = 'Esther'").toExpr("age < 32").run()
paths.show(false)

执行以上代码，输出结果如下：

+------------------------------+--------------+--------------------------------+
|from                               |e0               |to                              |
+------------------------------+--------------+--------------------------------+
|[e, Esther, 32, 1, Watermelon]|[e, d, friend]|[d, David, 29, 2321111, Bananas]|
+------------------------------+--------------+--------------------------------+

搜索还可以使用边过滤器和最大路径长度进行限制，代码如下：

val filteredPaths = g.bfs
      .fromExpr("name = 'Esther'").toExpr("age < 32")
      .edgeFilter("relationship != 'friend'")
      .maxPathLength(3)
      .run()
filteredPaths.show()

执行以上代码，输出结果如下：

+--------------------+--------------+--------------------+--------------+--------------------+
|                from|            e0|                  v1|            e1|                  to|
+--------------------+--------------+--------------------+--------------+--------------------+
|[e, Esther, 32, 1...|[e, f, follow]|[f, Fanny, 36, 33...|[f, c, follow]|[c, Charlie, 30, ...|
+--------------------+--------------+--------------------+--------------+--------------------+

例如，寻找从“现金超过20000元的人”到“年龄不到50岁”的“非朋友”的连接，代码如下：

val f = g.bfs
      .fromExpr("cash > 20000").toExpr("age < 50")
      .edgeFilter("relationship = 'follow'")
      .maxPathLength(3)
      .run()
f.show(false)
// f.filter("from.id != to.id").show(false)

执行以上代码，输出结果如下：

+--------------------------------+--------------------------------+
|from                                  |to                                    |
+--------------------------------+--------------------------------+
|[b, Bob, 36, 23232323, Bananas] |[b, Bob, 36, 23232323, Bananas] |
|[d, David, 29, 2321111, Bananas]|[d, David, 29, 2321111, Bananas]|
+--------------------------------+--------------------------------+

2. 连通分量算法

在图论中，无向图的一个组件（有时称为连通组件）是一个子图，其中任意两个顶点通过路径相互连接，并且在超图中不与任何其他的顶点连接。有三个组件的图如下图所示。

没有关联边的顶点本身就是一个组件。一个自身连通的图只有一个分量，由整个图组成。

连通分量算法寻找孤立的集群或孤立的子图。这些集群是图中的连接顶点的集合，其中每个顶点都可以从同一集合中的任何其他顶点到达。该算法返回一个包含每个顶点和该顶点所在连通组件的GraphFrame，代码如下：

// 设置检查点
spark.sparkContext.setCheckpointDir("tmp/gfcc")
val result = g.connectedComponents.run()   
result.show()

注意： 对于GraphFrames 0.3.0及以后的版本，默认的连通分量算法需要设置一个Spark检查点目录。

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+------------+
| id|   name|age|    cash|     fruit|   component|
+---+-------+---+--------+----------+------------+
|  a|  Alice| 34|     234|    Apples|412316860416|
|  b|    Bob| 36|23232323|   Bananas|412316860416|
|  c|Charlie| 30|    2123|Grapefruit|412316860416|
|  d|  David| 29| 2321111|   Bananas|412316860416|
|  e| Esther| 32|       1|Watermelon|412316860416|
|  f|  Fanny| 36|     333|    Apples|412316860416|
|  g|  Gabby| 60|   23433|   Oranges|146028888064|
+---+-------+---+--------+----------+------------+

3. 强连通分量算法

在有向图的数学理论中，如果一个图的每个顶点都能从其他顶点到达，那么这个图就被称为强连通图。任意有向图的强连通分量构成子图的划分，子图本身是强连通的。在线性时间内，可以测试图的强连通性，或者找到它的强连通部分。

如果有向图的每对顶点之间在每个方向上都有一条路径，则称为强连通图。也就是说，从第一个顶点到第二个顶点存在一条路径，从第二个顶点到第一个顶点存在另一条路径。强连接图的概念如下图所示。

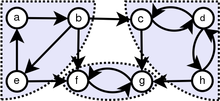
强连通分量算法计算每个顶点的强连通分量（SCC），并返回一个图，其中每个顶点分配给包含该顶点的SCC，代码如下：

val result = g.stronglyConnectedComponents.maxIter(10).run()
result.orderBy("component").show()

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+-------------+
| id|   name|age|     cash|      fruit|     component|
+---+-------+---+--------+----------+-------------+
|  g|   Gabby| 60|   23433|    Oranges| 146028888064|
|  f|   Fanny| 36|     333|     Apples| 412316860416|
|  e|  Esther| 32|       1| Watermelon| 670014898176|
|  d|   David| 29| 2321111|   Bananas| 670014898176|
|  a|   Alice| 34|     234|     Apples| 670014898176|
|  c|Charlie| 30|    2123|Grapefruit| 1047972020224|
|  b|     Bob| 36|23232323|   Bananas| 1382979469312|
+---+-------+---+--------+----------+-------------+

4. 标签传播算法

标签传播是一种半监督机器学习算法，它将标签分配给之前未标记的数据点。在算法开始时，数据点的一个（通常很小的）子集有标签（或分类）。这些标签将在整个算法过程中传播到未标记的点。

标签传播算法（Label Propagation Algorithm（LPA））运行静态标签传播算法来检测网络中的社区。

网络中的每个节点最初都被分配给它自己的社区。在每个superstep中，节点将它们的社区从属关系发送给所有邻居，并将它们的状态更新为传入消息的模式社区从属关系。

LPA是一种标准的图社区检测算法。它的计算成本非常低，尽管(1)不能保证收敛，(2)最终可能得到简单的解决方案（所有节点都被标识为单个社区）。代码如下：

val result = g.labelPropagation.maxIter(5).run()
result.orderBy("label").show()

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+-------------+
| id|   name|age|      cash|     fruit|          label|
+---+-------+---+--------+----------+-------------+
|  g|  Gabby| 60|     23433|   Oranges| 146028888064|
|  d|  David| 29|  2321111|   Bananas| 670014898176|
|  e| Esther| 32|         1|Watermelon| 670014898176|
|  c|Charlie| 30|      2123|Grapefruit|1047972020224|
|  b|    Bob| 36| 23232323|   Bananas|1382979469312|
|  f|  Fanny| 36|       333|    Apples|1460288880640|
|  a|  Alice| 34|       234|    Apples|1460288880640|
+---+-------+---+--------+----------+-------------+

5. PageRank算法

PageRank是谷歌搜索引擎使用的一种算法，用于在搜索引擎结果中对网页进行排名。它用节点代表网页，用边代表网页间的链接，并按链接页面的数量和排名加上每个链接的页面的数量和排名计算页面重要性。根据Google的描述："PageRank通过计算链接的数量和质量来粗略估计网站的重要性。潜在的假设是，更重要的网站有可能收到更多来自其他网站的链接。"

PageRank是以谷歌的创始人之一Larry Page的名字命名的。PageRank是衡量网站页面重要性的一种方法。PageRank算法在测量图中某个顶点的重要性时非常有用。

在GraphFrames中，PageRank算法有两种实现：

• (1) 第一种实现使用org.apache.spark.graphx.graph接口与aggregateMessages()方法，并运行PageRank为固定的迭代次数。这可以通过设置maxIter参数来执行。
• (2) 第二种实现使用org.apache.spark.graphx.Pregel，并运行PageRank，直到收敛，这可以通过设置tol参数来运行。

这两种实现都支持非个性化和个性化PageRank，其中设置sourceId将对该顶点的结果进行个性化处理。

例如，运行PageRank，识别图中的重要顶点，代码如下：

import org.apache.spark.sql.functions._

// resetProbability和tol是收敛参数
val results = g.pageRank.resetProbability(0.15).tol(0.01).run()

results.vertices.orderBy(desc("pagerank")).show()
results.edges.orderBy(desc("weight")).show()

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+-------------------+
| id|   name|age|     cash|      fruit|             pagerank|
+---+-------+---+--------+----------+-------------------+
|  c|Charlie| 30|     2123|Grapefruit| 2.6878300011606218|
|  b|    Bob| 36| 23232323|   Bananas|   2.655507832863289|
|  a|  Alice| 34|       234|    Apples|0.44910633706538744|
|  e| Esther| 32|        1|Watermelon|0.37085233187676075|
|  d|  David| 29|  2321111|   Bananas| 0.3283606792049851|
|  f|  Fanny| 36|       333|    Apples| 0.3283606792049851|
|  g|  Gabby| 60|    23433|   Oranges| 0.1799821386239711|
+---+-------+---+--------+----------+-------------------+

+---+---+------------+------+
|src|dst|relationship|weight|
+---+---+------------+------+
|  c|  b|        follow|   1.0|
|  b|  c|        follow|   1.0|
|  d|  a|        friend|   1.0|
|  f|  c|        follow|   1.0|
|  a|  b|        friend|   0.5|
|  a|  e|        friend|   0.5|
|  e|  f|        follow|   0.5|
|  e|  d|        friend|   0.5|
+---+---+------------+------+

对固定次数的迭代运行PageRank，代码如下：

val results2 = g.pageRank.resetProbability(0.15).maxIter(10).run()

results2.vertices.orderBy(desc("pagerank")).show()
results2.edges.orderBy(desc("weight")).show()

其中：

• (1) maxIter()：要运行的页面排名的迭代次数，推荐值为20，太少会降低质量，太多会降低性能。
• (2) resetProbability()：随机重置概率(alpha)-它越低，分数差距就越大-有效范围从0到1。通常，0.15是一个不错的分数。

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+-------------------+
| id|   name|age|     cash|      fruit|             pagerank|
+---+-------+---+--------+----------+-------------------+
|  b|     Bob| 36|23232323|   Bananas| 2.7025217677349773|
|  c|Charlie| 30|     2123|Grapefruit| 2.6667877057849627|
|  a|  Alice| 34|      234|     Apples| 0.4485115093698443|
|  e| Esther| 32|        1|Watermelon| 0.3613490987992571|
|  f|  Fanny| 36|      333|     Apples|0.32504910549694244|
|  d|  David| 29| 2321111|    Bananas|0.32504910549694244|
|  g|  Gabby| 60|    23433|    Oranges|0.17073170731707318|
+---+-------+---+--------+----------+-------------------+

+---+---+------------+------+
|src|dst|relationship|weight|
+---+---+------------+------+
|  c|   b|       follow|   1.0|
|  b|   c|       follow|   1.0|
|  d|   a|       friend|   1.0|
|  f|   c|       follow|   1.0|
|  a|   b|       friend|   0.5|
|  e|   d|       friend|   0.5|
|  a|   e|       friend|   0.5|
|  e|   f|       follow|   0.5|
+---+---+------------+------+

为顶点a运行个性化的PageRank，代码如下：

val results3 = g
      .pageRank
      .resetProbability(0.15)
      .maxIter(10)
      .sourceId("a")
      .run()

results3.vertices.show()

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+-------------------+
| id|   name| age|    cash|      fruit|             pagerank|
+---+-------+---+--------+----------+-------------------+
|  b|     Bob| 36|23232323|    Bananas| 0.3366143039702568|
|  e| Esther| 32|         1|Watermelon|0.07657840357273027|
|  a|  Alice| 34|       234|    Apples|0.17710831642683564|
|  f|  Fanny| 36|       333|    Apples|0.03189213697274781|
|  g|  Gabby| 60|     23433|   Oranges|                   0.0|
|  d|  David| 29|  2321111|   Bananas|0.03189213697274781|
|  c|Charlie| 30|     2123|Grapefruit| 0.3459147020846817|
+---+-------+---+--------+----------+-------------------+

对顶点["a", "b", "c", "d"]并行运行个性化的PageRank，代码如下：

val ids = Array("a", "b", "c", "d").asInstanceOf[Array[Any]]
val results3 = g
      .parallelPersonalizedPageRank
      .resetProbability(0.15)
      .maxIter(10)
      .sourceIds(ids)
      .run()
results3.vertices.show()

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+--------------------+
| id|   name|age|     cash|      fruit|             pageranks|
+---+-------+---+--------+----------+--------------------+
|  b|     Bob| 36|23232323|   Bananas|(4,[0,1,2,3],[0.3...|
|  e| Esther| 32|         1|Watermelon|(4,[0,1,2,3],[0.0...|
|  a|   Alice| 34|      234|    Apples|(4,[0,1,2,3],[0.1...|
|  f|   Fanny| 36|      333|    Apples|(4,[0,1,2,3],[0.0...|
|  g|   Gabby| 60|    23433|   Oranges|(4,[0,1,2,3],[0.0...|
|  d|   David| 29| 2321111|   Bananas|(4,[0,1,2,3],[0.0...|
|  c| Charlie| 30|    2123|Grapefruit|(4,[0,1,2,3],[0.3...|
+---+-------+---+--------+----------+--------------------+

6. 最短路径算法

在图论中，最短路径问题是在图中两个顶点之间找到一条路径，使其组成边的权值之和最小。对于有向图，路径的定义要求连续的顶点由合适的有向边连接。例如，一个加权有向图，图中顶点A和F之间的最短路径是（A，C，E，D，F），如下图所示。

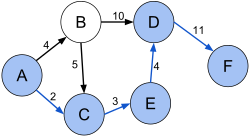
GraphFrames中最短路径算法实现是shortestPaths，它计算从每个顶点到给定的地标顶点集的最短路径（但是不考虑权值），地标由顶点ID指定。注意，这考虑了边的方向。

例如，计算图中每个顶点到地标顶点a和d之间的最短路径，代码如下：

val paths = g.shortestPaths.landmarks(Seq("a", "d")).run()
paths.show(false)

执行以上代码，输出结果如下：

+---+-------+---+--------+----------+----------------+
|id | name   |age|cash    |fruit      |distances         |
+---+-------+---+--------+----------+----------------+
|b  |Bob     |36 |23232323|Bananas   |[]                  |
|e  |Esther |32 |1        |Watermelon|[d -> 1, a -> 2] |
|a  |Alice  |34 |234      |Apples     |[a -> 0, d -> 2] |
|f  |Fanny  |36 |333      |Apples     |[]                  |
|g  |Gabby  |60 |23433    |Oranges   |[]                  |
|d  |David  |29 |2321111 |Bananas    |[d -> 0, a -> 1] |
|c  |Charlie|30 |2123    |Grapefruit |[]                 |
+---+-------+---+--------+----------+----------------+

进一步进行条件过滤，代码如下：

paths.filter(col("distances")("d") > 0).show(false)
paths.filter(size(map_keys(col("distances")))=!=0).show(false)

执行以上代码，输出结果如下：

+---+------+---+----+----------+----------------+
|id |name  |age|cash|fruit      |distances         |
+---+------+---+----+----------+----------------+
|e  |Esther|32 |1   |Watermelon|[d -> 1, a -> 2]|
|a  |Alice |34 |234 |Apples    |[a -> 0, d -> 2]|
+---+------+---+----+----------+----------------+

+---+------+---+-------+----------+----------------+
|id |name  |age|cash    |fruit      |distances        |
+---+------+---+-------+----------+----------------+
|e  |Esther|32 |1       |Watermelon|[d -> 1, a -> 2]|
|a  |Alice |34 |234     |Apples     |[a -> 0, d -> 2]|
|d  |David |29 |2321111|Bananas    |[d -> 0, a -> 1]|
+---+------+---+-------+----------+----------------+

7. 三角计数算法

顶点三角形计数算法是一种社区检测图算法，用于计算图中每个顶点所属的三角形的数量。三角形被定义为由三条边（a-b，b-c，c-a）连接的三个节点，其中每个顶点都与三角形中的其他两个顶点有关系。在一个图中，如果一条边的两个点如果有共同邻居点，那么这三个点就构成了三角形结构。例如，一个顶点三角表结构示例如下图所示。

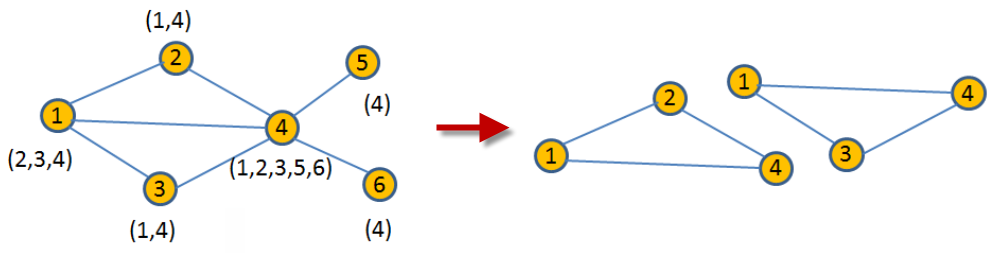
在上图中，左边的图中可找出两个三角形结构，分别是1-2-3和1-4-3。

三角计数在社交网络分析中很受欢迎，它被用来检测社区并测量这些社区的凝聚力。它也可以用来确定一个图的稳定性，并经常被用作计算网络指标的一部分，如聚类系数。采用三角形计数算法计算局部聚类系数。

在GraphFrames中，通过triangleCount实现了该算法，它返回一个GraphFrame，其中包含通过每个顶点的三角形数量。

例如，计算图g中通过每个顶点的三角形的数量，代码如下：

val results = g.triangleCount.run()
results.select("id", "count").show()

执行以上代码，输出结果如下：

+---+-----+
| id|count|
+---+-----+
|  g|     0|
|  f|     0|
|  e|     1|
|  d|     1|
|  c|     0|
|  b|     0|
|  a|     1|
+---+-----+