使用GraphX Pregel API
图本身是递归数据结构,顶点的属性依赖于它们邻居的属性,这些邻居的属性又依赖于自己邻居的属性。所以许多重要的图算法都是迭代的重新计算每个顶点的属性,直到满足某个确定的条件。
Pregel是一种面向图算法的分布式编程框架,采用迭代的计算模型:在每一轮,每个顶点处理上一轮收到的消息,并发出消息给其它顶点,并更新自身状态和拓扑结构(出、入边)等。GraphX实现了一个类似pregel的批量同步消息传递API,这是基于Bulk Synchronous Parallel (BSP,分布式批同步) 算法的。
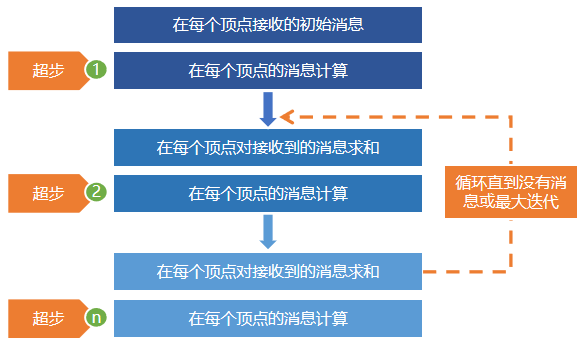
GraphX中实现的这个更高级的Pregel操作是一个约束到图拓扑的批量同步(bulk-synchronous)并行消息抽象。Pregel操作符在一系列的超步(super steps)中执行。在每一次超步中,顶点的计算都是并行的,并且执行用户定义的同一个函数。每个顶点可以修改其自身的状态信息或以它为起点的出边的信息,从前序超步中接受消息,并传送给其后续超步,或者修改整个图的拓扑结构。边,在这种计算模式中并不是核心对象,没有相应的计算运行在其上。因此,在每一个超步中,总是按如下顺序执行:
- 顶点从上一个super step接收它们的入站(inbound)消息的总和;
- 为顶点属性计算一个新的值;
- 在下一个super step中向相邻的顶点发送消息。
消息通过边triplet的一个函数被并行计算,消息的计算既会访问源顶点特征也会访问目的顶点特征。在超步中,没有收到消息的顶点会被跳过。当没有消息遗留时,Pregel操作将结束迭代并返回最终的图。
Pregel计算模型中有三个重要的函数,分别是vertexProgram()、sendMessage()和messageCombiner()。
- vertexProgram:用户定义的顶点运行程序。它作用于每一个顶点,负责接收进来的信息,并计算新的顶点值。
- sendMsg:发送消息。
- mergeMsg:合并消息。
下面是使用Pregel API的一个示例。
import org.apache.spark.graphx._
import org.apache.spark.sql.SparkSession
......
// case class,用来代表顶点属性,存储一个用户的信息
case class User(name: String, age: Int)
def main(args: Array[String]): Unit = {
val spark = SparkSession.builder()
.master("local[*]")
.appName("graphx demo")
.getOrCreate()
// 构造顶点RDDs
val usersRDD = spark.sparkContext.parallelize(
List(
(1L, User("Alex", 26)),
(2L, User("Bill", 42)),
(3L, User("Carol", 18)),
(4L, User("Dave", 16)),
(5L, User("Eve", 45)),
(6L, User("Farell", 30)),
(7L, User("Garry", 32)),
(8L, User("Harry", 36)),
(9L, User("Ivan", 28)),
(10L, User("Jill", 48))
)
)
// 构造边RDDs
val followsRDD = spark.sparkContext.parallelize(
List(
Edge(1L, 2L, 1),
Edge(2L, 3L, 1),
Edge(3L, 1L, 1),
Edge(3L, 4L, 1),
Edge(3L, 5L, 1),
Edge(4L, 5L, 1),
Edge(6L, 5L, 1),
Edge(7L, 6L, 1),
Edge(6L, 8L, 1),
Edge(7L, 8L, 1),
Edge(7L, 9L, 1),
Edge(9L, 8L, 1),
Edge(8L, 10L, 1),
Edge(10L, 9L, 1),
Edge(1L, 11L, 1)
)
)
// 创建默认属性集(id为11的顶点没有任何属性)
// 它会将默认属性分配给没有被显式分配任何属性的顶点
val defaultUser = User("NA", 0)
// 构造图对象
val socialGraph = Graph(usersRDD, followsRDD, defaultUser)
// 根据从一个顶点的出度为每条边分配一个权重
val outDegrees = socialGraph.outDegrees
val outDegreesGraph = socialGraph.outerJoinVertices(outDegrees) {
(vId, vData, outDeg) => outDeg.getOrElse(0)
}
val weightedEdgesGraph = outDegreesGraph.mapTriplets{et => 1.0 / et.srcAttr }
// 接下来,为每个用户分配一个初始影响等级
val inputGraph = weightedEdgesGraph.mapVertices((id, vData) => 1.0)
// 初始化传递给pregel方法的参数
// 将传递给pregel方法的三个参数的第一个集合。
val firstMessage = 0.0
val iterations = 20
val edgeDirection = EdgeDirection.Out
// 接下来,定义作为参数传递给pregel方法的三个函数
val updateVertex = (vId: Long, vData: Double, msgSum: Double) => 0.15 + 0.85 * msgSum
val sendMsg = (triplet: EdgeTriplet[Double, Double]) => Iterator((triplet.dstId, triplet.srcAttr * triplet.attr))
val aggregateMsgs = (x: Double, y: Double ) => x + y
// 现在调用pregel方法
/* Pregel是一种分布式计算模型,用于处理具有数十亿顶点和数万亿条边的大型图形 */
val influenceGraph = inputGraph
.pregel(firstMessage, iterations, edgeDirection)(updateVertex, sendMsg, aggregateMsgs)
// 打印每个用户的姓名和影响排名来检查计算结果
val userNames = socialGraph.mapVertices{(vId, user) => user.name}.vertices
val userNamesAndRanks = influenceGraph
.outerJoinVertices(userNames){(vId, rank, optUserName) => (optUserName.get, rank)}
.vertices
userNamesAndRanks.collect.foreach{
case(vId, vData) => println(vData._1 +"的影响力: " + vData._2)
}
}
输出结果如下:
Harry的影响力: 0.9733813220346056 Alex的影响力: 0.2546939612521768 Ivan的影响力: 0.9670543985781628 Jill的影响力: 0.9718993399637271 Bill的影响力: 0.25824491587871073 NA的影响力: 0.25824491587871073 Carol的影响力: 0.36950816084343974 Dave的影响力: 0.2546939612521768 Eve的影响力: 0.47118379300959834 Farell的影响力: 0.1925 Garry的影响力: 0.15
注意,与标准的Pregel实现不同的是,GraphX的Pregel实现中的顶点仅仅能发送信息给邻居顶点,并且可以利用用户自定义的消息函数并行地构造消息。这些限制允许对GraphX进行额外的优化。
下面是另一个使用Pregel实现的图算法:最短路径算法。
import org.apache.spark.sql.SparkSession
import org.apache.spark.graphx._
import org.apache.spark.graphx.util.GraphGenerators
......
def main(args: Array[String]): Unit = {
val spark = SparkSession.builder()
.master("local[*]")
.appName("graphx demo")
.getOrCreate()
val graph = GraphGenerators
.logNormalGraph(spark.sparkContext, numVertices = 100)
.mapEdges(e => e.attr.toDouble)
val sourceId: VertexId = 42 // 最终的源
// 初始化图
val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
(id, dist, newDist) => math.min(dist, newDist), // Vertex Program
triplet => { // 发送消息
if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
} else {
Iterator.empty
}
},
(a,b) => math.min(a,b) // 合并消息
)
println(sssp.vertices.take(10).mkString("\n"))
}
输出结果如下所示:
(96,2.0) (56,2.0) (16,1.0) (80,2.0) (48,2.0) (32,2.0) (0,2.0) (24,2.0) (64,2.0) (40,1.0)
上面的例子中,Vertex Program函数定义如下:
(id, dist, newDist) => math.min(dist, newDist)
这个函数的定义显而易见,当两个消息来的时候,取它们当中路径的最小值。同理Merge Message函数也是同样的含义。
Send Message函数中,会首先比较triplet.srcAttr + triplet.attr和triplet.dstAttr,即比较加上边的属性后,这个值是否小于目的节点的属性,如果小于,则发送消息到目的顶点。
Pregel框架的缺点
这个模型虽然简单,但是缺陷明显,那就是对于邻居数很多的顶点,它需要处理的消息非常庞大,而且在这个模式下,它们是无法被并发处理的。所以对于符合幂律分布的自然图,这种计算模型下很容易发生假死或者崩溃。
